Answer:

Where

Explanation:
To find:
The equation of the given graph in the question area.
Solution:
By looking at the graph, we can clearly see that the graph is either sine curve or cosine curve.
We know that sine curve starts at 0.
Therefore, the given curve is sine curve.
Let us have a look at the different values of a sine curve at various angles.
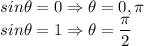
Also,
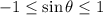
Here, we have
 at
at
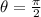 , it means that angle is in the form of
, it means that angle is in the form of
 .
.
Now, let us have a look at the curve is decreasing or increasing.
It is decreasing after the angle 0, therefore the function has a negative sign.
So, it can be written as:

Now, let us have a look at the maximum and minimum values so as to find the value of

Here, we can clearly see that minimum value is -2 and maximum value is 2.
Therefore, the value of
 is 2.
is 2.
So, the equation is:

Where
