Given:
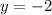
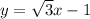
To find:
The obtuse angle between the given pair of straight lines.
Solution:
The slope intercept form of a line is
 ...(i)
...(i)
where, m is slope and b is y-intercept.
The given equations are
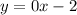
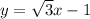
On comparing these equations with (i), we get
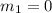
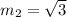
Angle between two lines whose slopes are
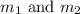 is
is
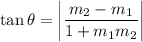
Putting
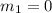 and
and
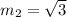 , we get
, we get
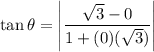
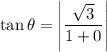
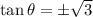
Now,
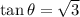 and
and
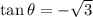
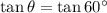 and
and

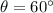 and
and
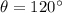
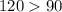 , so it is an obtuse angle and
, so it is an obtuse angle and
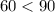 , so it is an acute angle.
, so it is an acute angle.
Therefore, the obtuse angle between the given pair of straight lines is 120°.