Question

What is the equation of the line that passes through the point (4.11) and is perpendicular to the line with the following equation? OA. y = -x + 14 O B. - r - 15 OD. & 1 + 8​

Answer 1

`y = x +7`

Explanation:

Given

`Point\ (x_1,y_1) = (4,11)`

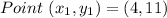
Perpendicular to
`y = -x + 14`

Required

Determine the line equation

An equation has the form

`y = mx + b`

Where

`m = slope`

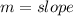
By comparison with
`y = -x + 14`

`m = -1`

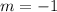
Because the line is perpendicular to
`y = -x + 14`, the following relationship exists

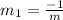`m_1 = (-1)/(m)` i.e. the condition for perpendicularity

Where m1 is the slope of the equation that passes through
`Point\ (x_1,y_1) = (4,11)`

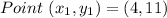
So, we have:

`m_1 = (-1)/(-1)`

`m_1 = 1`

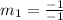
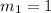
The line equation is then calculated using:

`y - y_1 = m_1(x - x_1)`

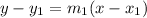
Where

`m_1 = 1`

`Point\ (x_1,y_1) = (4,11)`

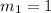
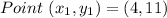
So, we have:

`y - 11 = 1(x - 4)`

`y - 11 = x - 4`

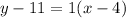
Add 11 to both sides

`y - 11+11 = x - 4+11`

`y = x - 4+11`

`y = x +7`

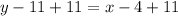
The B, C and D parts of your question are not clear.

Apply the same steps used in (a) above and you'll get your answers