Answer:
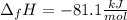
Step-by-step explanation:
Hello!
In this case, since the enthalpy of formation of ethane at 298 K is about -84 kJ/mol, via the Kirkoff's law, we can compute it a 350 K as shown below:
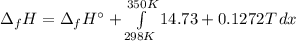
It means we can integrate to get:
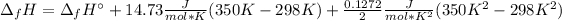
Now, we can plug in the enthalpy of formation in consistent units to obtain:
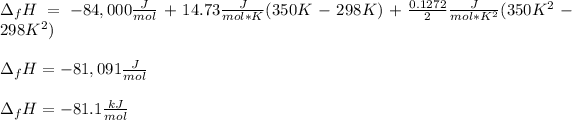
Best regards!