Question

Question 18

Look at this sequence.

95, 80, 65, 50, ...
Which function represents this sequence?

A
a(n)=−15n+110

B
a(n)=110n−15

C
a(n)=95n−15

D
a(n)=−15n+95

Answer 1

The function which represents this sequence will be:

`a_n=-15n+110`

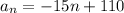
Hence, option (A) is true.

Explanation:

Given the sequence

`95, 80, 65, 50, ...`

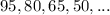
An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

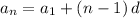
computing the differences of all the adjacent terms

`80-95=-15,\:\quad \:65-80=-15,\:\quad \:50-65=-15`

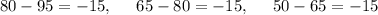
As the difference is the same, so

`d = -15`

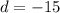
as

`a_1=95`

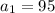
Thus, substituting
`d = -15`,
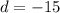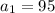`a_1=95` in the nth term of an arithmetic sequence

`a_n=a_1+\left(n-1\right)d`

`a_n=-15\left(n-1\right)+95`

`a_n=-15n+110`

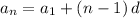
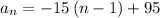
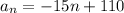
Therefore, the function which represents this sequence will be:

`a_n=-15n+110`

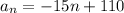
Hence, option (A) is true.