Answer:
See the answers below
Step-by-step explanation:
This problem and its respective questions can be easily solved using Newton's law of universal gravitation. Which can be calculated by means of the following expression.
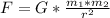
where:
G = it is the universal gravitation constant. = 6.673 x 10⁻¹¹ [N*m²/kg²]
m1 = mass of the first body [kg]
m2 = mass of the second body [kg]
r = distance among the bodies [m]
a. the mass of one is doubled?
When this happens we see that the force is increased twice as well, since the mass is in the numerator of the expression.
b. The masses of both are doubled?
If both masses are doubled the force is increased to four times its original value since the terms of the masses are in the numerator of the expression.
c. The distance between them is doubled?
In this case the force is decreased to half of its original value, since the distance is in the denominator of the expression of universal gravitation.