Question

For x such that 0 < x < ~, the expression V1 - cos x + V1 - sin x is equivalent to: sin x COS X F. 0 G. 1 H. 2 J. -tan x K. Sin 2x

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The correct option is H

Explanation:

From the question we are told that

The equation is
`(√(1 - cos^2 (x)) )/(sin(x)) + (√(1 - sin^2 (x)) )/(cos(x))`

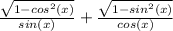
The domain for x is
`0 < x < (\pi)/(2)`

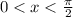
Gnerally the equation above is not continuous, when

`sin (x) = 0`

=>
`x = 0`

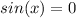
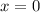
And when
`cos(x) = 0`

=>
`x = (\pi)/(2)`

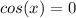
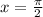
Generally from trigonometry identity

`sin^2x + cos^2 x = 1`

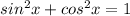
So

`sin^2 x = 1 - cos^2 (x)`

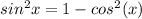
So

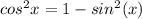
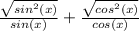
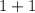
`cos^2 x = 1 - sin^2 (x)`

=>
`(√(sin^2 (x)) )/(sin(x)) + (√( cos^2 (x )) )/(cos(x))`

=>
`1 + 1`

=>
`2`