Answer:
The value of a = 14
Explanation:
Given
(x₁, y₁) = (2, 4)
(x₂, y₂) = (6, a)
(x₃, y₃) = (-1, 1)
A = 9 sq.units
Area of a triangle with vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) is:
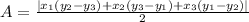
substituting the values (x₁, y₁) = (2, 4), (x₂, y₂) = (6, a), (x₃, y₃) = (-1, 1), A = 9 in th formula
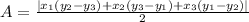
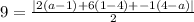
Multiply both sides by 2
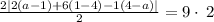
simplify

As the area is always positive.
so
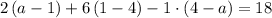

Add 18 to both sides
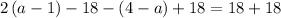
simplify

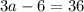
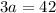
Divide both sides by 3
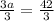
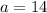
Thus, the value of a = 14