Question

For a study of adolescents' disclosure of their dating and romantic relationships, a sample of 224 high school students was surveyed. One of the variables of interest was the level of disclosure to an adolescent's mother (measured on a 5-point scale, where 1 = "never tell" and 5 ="always tell"). The sampled high school students had a mean disclosure score of 3.38 and a standard deviation of 0.98. The researchers hypothesize that the true mean disclosure score of all adolescents will exceed 3. Do you believe the researchers?

Conduct a formal test of hypothesis using α = 0.05. Set

Answer 1

The decision rule is

Reject the null hypothesis

The conclusion is

There sufficient evidence that the true mean disclosure score of all adolescents will exceed 3

Explanation:

From the question we are told that

The sample is n = 224

The sample mean is
`\= x = 3.38`

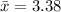
The standard deviation is
`s = 0.98`

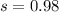
The population mean is
`\mu = 3`

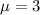
The level of significance is
`\alpha = 0.05`

The null hypothesis is
`H_o : \mu = 3`

The alternative hypothesis is
`H_a : \mu > 3`

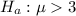
Generally the test statistics is mathematically represented as

`z = ( \= x - \mu )/( (s)/( √(n) ) )`

=>
`z = ( 3.38 - 3 )/( (0.98 )/( √(224) ) )`

=>
`z = 5.80`

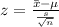
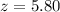
From the z table the area under the normal curve to the right corresponding to 5.80 is

`p-value = 0`

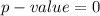
From the value obtained we that
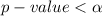`p-value < \alpha` , hence

The decision rule is

Reject the null hypothesis

The conclusion is

There sufficient evidence that the true mean disclosure score of all adolescents will exceed 3