Solution :
Given :
Mass attached to the spring = 4 kg
Mass dropped = 6 kg
Force constant = 100 N/m
Initial amplitude = 2 m
Therefore,
a).


= 10 m/s
Final velocity, v at equilibrium position, v = 5 m/s
Now,
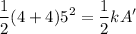
A' = amplitude = 1.4142 m
b).

m' = 2m
Hence,
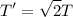
c).


Therefore, factor

Thus, the energy will change half times as the result of the collision.