Question

We are designing gift bags of fruit, and a bag is supposed to contain 30 pieces of fruit. Find the number of bags of fruit that can be made out of apples, bananas, oranges, and pears, where, in each bag, the number of apples is even, the number of bananas is a multiple of 5, the number of oranges is at most 4, and the number of pears is 0 or 1.

a. What if the 30 were replaced by n?
b. Is there a formula for the number of bags with n pieces of fruit that obey these rules?

Answer 1

Explanation:

For each type of fruit, the corresponding generating function will be:

For apples the generating function will be:

For banana the generating function will be:

For orange the generating function will be:

`\sum_(e 3=0)^(\infty) x^{e^(3)} &=1+x+x^(2)+x^(3)+x^(4)+\ldots \ldots \\</p><p>&=(1-x^(5))/(1-x)`

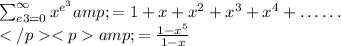
For pears the generating function will be :

Then the generating function is the product of the factors:

`={c}</p><p>n+2-1\\</p><p>n \\`

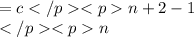
Therefore, we get

From the given question data,

`h_(n) &=n+1 \\</p><p>&=30+1 \\</p><p>&=31`

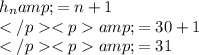
CONCLUSION：

For h_{n} the value n=30 is the answer.