Answer:
Explanation:
From the question we are told that
The first sample size is
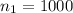
The second sample size is
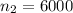
The number that had significant outside activity in the sample with ALL is

The number that had significant outside activity in the sample without ALL is
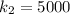
Considering question a
The percentage of children with ALL have significant social activity outside the home when younger is mathematically represented as
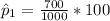
=>
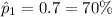
Considering question b
The percentage of children without ALL have significant social activity outside the home when younger is mathematically represented as
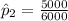
=>
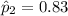
Generally the sample odds ratio for significant social activity outside the home when younger, comparing the groups with and without ALL is mathematically represented as

=>

=>
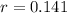
Considering question c
From the question we are told the confidence level is 95% , hence the level of significance is
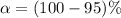
=>

Generally from the normal distribution table the critical value of
 is
is
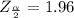
Generally the lower limit of the 95% confidence interval for the population odds ratio for significant social activity outside the home when younger, comparing the groups with and without ALL is mathematically represented as
![a = e^{ln ( r ) - Z_{(\alpha )/(2)} \sqrt{ [ (1)/( k_1 ) ] + [ (1)/( c_1 ) ] + [(1)/(k_2) ] + [(1)/( c_2 ) ] } }](https://img.qammunity.org/2021/formulas/mathematics/college/aexp3lp0712qavsot7fyr6i4mta16o67lh.png)
Here
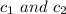 are the non-significant values i.e people that did not play outside when they were young in both samples
are the non-significant values i.e people that did not play outside when they were young in both samples
The values are

and
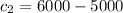
=>
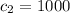
=>
![a = e^{ln ( 0.141 ) - 1.96 \sqrt{ [ (1)/( 700 ) ] + [ (1)/( 1000) ] + [(1)/(5000) ] + [(1)/( 300 ) ] } }](https://img.qammunity.org/2021/formulas/mathematics/college/dl3uv4pulgppl5kuoynd5ui0q7j11ss4m0.png)
=>
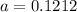
Generally the upper limit of the 95% confidence interval for the population odds ratio for significant social activity outside the home when younger, comparing the groups with and without ALL is mathematically represented as
![b = e^{ln ( 0.141 ) + 1.96 \sqrt{ [ (1)/( 700 ) ] + [ (1)/( 1000) ] + [(1)/(5000) ] + [(1)/( 300 ) ] } }](https://img.qammunity.org/2021/formulas/mathematics/college/tw4qo4xcspr86g0fvgltj7uohc46tanr59.png)
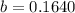
Generally the 95% confidence interval for the population odds ratio for significant social activity outside the home when younger, comparing the groups with and without ALL is
![95\% CI = [ 0.1212 , 0.1640 ]](https://img.qammunity.org/2021/formulas/mathematics/college/oruidfomt6k2ah9mmeizl0uwywr08q03v9.png)
Generally looking and the confidence interval obtained we see that it is less that 1 hence this means that there is a greater odd of developing ALL in groups with insignificant social activity compared to groups with significant social activity