Answer:
Step-by-step explanation:
(a)
From the given information:
The initial velocity
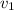 = 5 m/s
= 5 m/s
The direction of the angle θ = 30°
Therefore, the component along the x-axis =
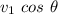
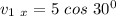
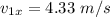
The component along the y-axis =
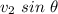
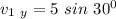
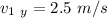
To find the final velocity( reflected velocity)
using the same magnitude
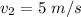
The angle from the x-axis can be
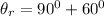
= 150°
Thus, the component along the x-axis =
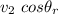
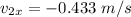
The component along the y-axis =
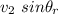
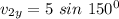
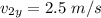
(b)
The velocity
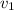 can be written as in vector form.
can be written as in vector form.
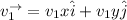
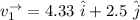 ---- (1)
---- (1)
The reflected velocity in vector form can be computed as:
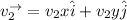
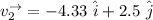 --- (2)
--- (2)
The change in velocity =

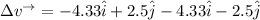
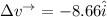
(c)
The magnitude of change in velocity =
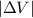
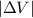 = 8.66 m/s
= 8.66 m/s