Question

The amount of time devoted to studying statistics each week by students who achieve a

grade of A in the course is normally distributed with a mean of 7.5 hours and a standard

deviation of 2.1 hours.

a. What proportion of A students study for more than 10 hours per week.

b. Find the probability that an A student spends between 7 and 9 hour​

Answer 1

a) the probability of A students study for more than 10 hours per week

P(X>10) = 0.117

b) The probability that an student spends between 7 and 9 hour

P(7<x< 9) = 0.9522

Explanation:

Step(I):-

Let 'X' be random variable of the normal distributed with a mean of 7.5 hours and standard deviation of 2.1 hours

mean of the Population is = 7.5 hours

standard deviation of the Population = 2.1 hours

`Z = (x-mean)/(S.D)`

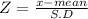
Z = 1.1904

The probability of A students study for more than 10 hours per week

P(X>10) = 0.5-A(Z₁) = 0.5 -A(1.1904) = 0.5 - 0.3830 = 0.117

Step(ii):-

Put x=7

`Z = (7-7.5)/(2.1)= -0.238`

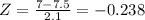
put x=9

`Z = (9-7.5)/(2.1) = 0.7142`

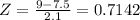
The probability that an A student spends between 7 and 9 hour

P(7 < x< 9) = A(9) - A(7)

= 0.7142 +0.238

= 0.9522