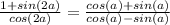Question

1+ sin2a/cos2a


`(1 + sin2 \alpha )/(cos2 \alpha )`
​

Answer 1

`(1 + sin(2 a))/(cos(2 a) ) = (cos(a)+ sin(a))/(cos(a) - sin(a) )`

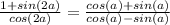
Explanation:

The question is incomplete; however, I'll simplify the given expression as far as it can be simplified.

Given

`(1 + sin(2 a))/(cos(2 a) )`

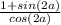
Required

Simplify

`(1 + sin(2 a))/(cos(2 a) )`

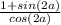
In trigonometry:

`sin(2a) = 2sin(a)cos(a)`

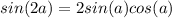
So, the expression becomes:

`(1 + 2sin(a)(cos(a))/(cos(2 a) )`

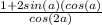
Also in trigonometry:

`cos^2(a) + sin^2(a) = 1`

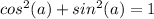
So, the expression becomes:

`(cos^2(a) + sin^2(a) + 2sin(a)(cos(a))/(cos(2 a) )`

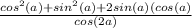
Also:

`cos(2a) = cos^2(a) - sin^2(a)`

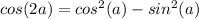
So, we have:

`(cos^2(a) + sin^2(a) + 2sin(a)(cos(a))/(cos^2(a) - sin^2(a) )`

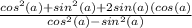
Rearrange the numerator:

`(cos^2(a) + 2sin(a)cos(a) + sin^2(a))/(cos^2(a) - sin^2(a) )`

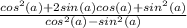
Expand the numerator

`(cos^2(a) + sin(a)cos(a)+ sin(a)cos(a) + sin^2(a))/(cos^2(a) - sin^2(a) )`

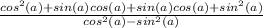
Factorize:

`(cos(a)(cos(a) + sin(a))+sin(a)(cos(a)+ sin(a)))/(cos^2(a) - sin^2(a) )`

`((cos(a) + sin(a))(cos(a)+ sin(a)))/(cos^2(a) - sin^2(a) )`

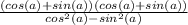
Apply difference of two squares to the denominator

`((cos(a) + sin(a))(cos(a)+ sin(a)))/((cos(a) - sin(a))(cos(a) + sin(a)) )`

Divide the numerator and denominator by
`cos(a) + sin(a)`

`(cos(a)+ sin(a))/(cos(a) - sin(a) )`

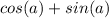
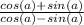
Hence:

`(1 + sin(2 a))/(cos(2 a) ) = (cos(a)+ sin(a))/(cos(a) - sin(a) )`