Answer:
From the question we are told that
The population mean is

The sample size is n = 30
The sample mean is
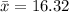
The population standard deviation is

The level of significance is
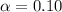
Step 1: State hypotheses:
The null hypothesis is
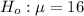
The alternative hypothesis is
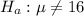
Step 2: State the test statistic. Since we know the population standard deviation and the sample is large our test statistics is
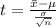
=>
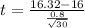
=>
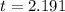
Generally the degree of freedom is mathematically represented as
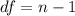
=>
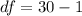
=>
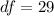
Step 3: State the critical region(s):
From the student t-distribution table the critical value corresponding to
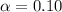 is
is
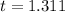
Generally the critical regions is mathematically represented as

Step 4: Conduct the experiment/study:
Generally the from the value obtained we see that the t value is outside the critical region so the decision is [Reject the null hypothesis ]
Step 5: Reach conclusions and state in English:
There is sufficient evidence to show that the filling weight has to be adjusted
Step 6: Calculate the p-value associated with this test. How does this the p-value support your conclusions in Step 5?
From the student t-distribution table the probability value to the right corresponding to
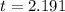 at a degree of freedom of
at a degree of freedom of
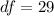 is
is

Generally the p-value is mathematically represented as

=>
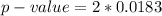
=>
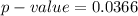
Generally looking at the value obtained we see that
 hence
hence
The decision rule is
Reject the null hypothesis
Explanation: