Answer:
The force is now 9 times the original force
Step-by-step explanation:
Coulomb's Law
The electrostatic force between two charged particles is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
Coulomb's formula is:

Where:
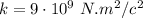
q1, q2 = the particles' charge
d= The distance between the particles
Suppose the distance is reduced to d'=d/3, the new force F' is:
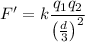
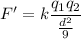
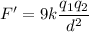

The force is now 9 times the original force