Question

In a giant swing, the seat is connected to two cables as shown, one (B) horizontal and the other 40o angle with the vertical (A). The chair swings in a horizontal circle at a speed of 32 revolutions per minute. If the seat weighs 255 N and a person weighing 825-N is sitting in it, find the tension on cable B. (g = 9,8 m / s2)

Answer 1

The tension in the cable B is approximately 8375.227 N

Step-by-step explanation:

The given parameters are;

The orientation of one cable, B = Horizontal

The orientation of the other cable, A = 40° to the vertical

The horizontal speed with which the chair swings= 32 revolutions per minute

ω = 32×2×π/60 rad /s

The weight of the seat = 255 N

The weight of the person = 825 N

The acceleration due to gravity, g = 9.8 m/s²

Therefore, we have;

The centripetal force
`F_c = \left (m_p + m_s \right ) * l * \omega ^2`, which gives;

`F_c = \left ((825 + 255)/(9.8) \right ) * 7.5 * \left ((32* 2 * \pi)/(60) \right )^2 \approx 9281.457`

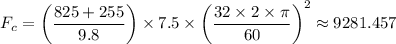
The weight of the person and the seat W = 825 + 255 = 1080 N = The vertical force component in the system

The vertical component of the cable A = The vertical force component in the system = 1080 N

Let
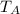`T_A` represent the tension in A

The vertical component of the tension =
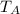`T_A` × cos 40° = 1080

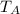`T_A` = 1080/(cos(40°)) ≈ 1409.84 N

The horizontal component of
`T_A` =

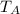From ∑Fₓ = 0, given that the centripetal force is acting outwards and the tension in cable B and the horizontal component of
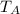`T_A` are acting inwards, we have;

The centripetal force,
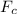`F_c` = The tension in the cable B + The horizontal component of
`T_A`

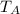
9281.457 = The tension in the cable B + 906.23

The tension in the cable B = 9281.457 - 906.23 ≈ 8375.227 N.