Answer:
Following are the solution to the given choices:
Explanation:
Given value:
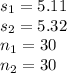
In point a:
Null hypothesis:
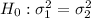
VS
Alternative:
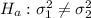
In point b:
Testing the statistic:

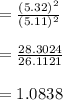
In point c:
Calculating the p-value, and the chances of rejection of
 :
:
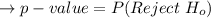
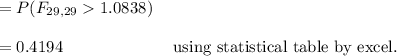
The
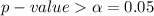 ,
,
 is not rejected at the level of
is not rejected at the level of
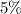 .
.
In point d:
Higher H0 must not be refused. It's indeed clear that perhaps the claim that the shift in maximum skull sizes is 4000 B.C is supported by sufficient evidence. The variation in A.D is the same. 150.