Question

Salmon often jump waterfalls to reach their breeding grounds. One salmon starts 2.00m from a waterfall that is 0.55m

tall and jumps at an angle of 32.0 degrees. What must be the salmon's minimum speed to reach the waterfall?

Answer 1

The salmon reaches the waterfall with a minimum speed of approximately 20.343 m/s

Step-by-step explanation:

The given parameters are;

The horizontal distance from the waterfall where the salmon starts to jump = 2.00 m

The height of the waterfall, h = 0.55 m

The angle (to the horizontal) at which the salmon jumps, θ = 32°

From
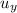`u_y`² = 2·g·h, we have;

Where;

g = The acceleration due to gravity = 9.8 m/s²

The minimum vertical velocity required,
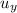`u_y` is given as follows;

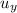`u_y` = √(2·g·h) = √(2 × 9.8 m/s² × 0.55 m) = 10.78 m/s

The minimum time, t, it will take the salmon to reach the height of the water fall is given as follows;

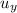`u_y` = gt

t =
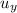`u_y`.g = 10.78/9.8 = 1.1 seconds

The vertical velocity
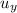`u_y` = u × sin(θ)

Therefore, the initial velocity, u =
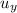`u_y`/sin(θ) = 10.78/(sin(32°)) ≈ 20.343 m/s

The horizontal component of the initial speed = 20.343 m/s × cos(32°) ≈ 17.252 m/s

Therefore, the horizontal distance covered in the 1.1 seconds = 1.1 × 17.252 = 18.9772 meters, which is larger than the 2.00 m distance from the waterfall, therefore, the salmon reaches the waterfall with a minimum speed of 20.343 m/s