Answer:
It will take approximately 34.13 years
Explanation:
The function G(t) below represents the amount of money in some account t years after the account is opened for The Johnson's daughter Gabriella:

It's required to find the number of years (t) it will take for the account to reach G(t)=150,000. We need to solve the equation:
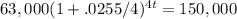
Dividing by 63,000 and simplifying:
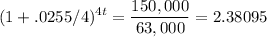
Taking logarithms:
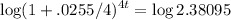
Applying logarithms property:
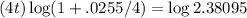
Solving for t:

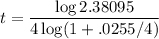
Calculating:

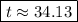
It will take approximately 34.13 years