Question

3х + бу
бу =
18 and Зу = - 5х + 9
do these have one solution,ims,or no solution

Answer 1

The solution of the system of equations will be:

`x=0,\:y=3`

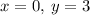
And the system of equations has ONLY ONE solution.

Explanation:

Given the system of the equations

`\begin{bmatrix}3x+6y=18\\ 3y=-5x+9\end{bmatrix}`

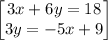
Arrange equation variables for elimination

`\begin{bmatrix}3x+6y=18\\ 5x+3y=9\end{bmatrix}`

`\mathrm{Multiply\:}3x+6y=18\mathrm{\:by\:}5\:\mathrm{:}\:\quad \:15x+30y=90`

`\mathrm{Multiply\:}5x+3y=9\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:15x+9y=27`

`\begin{bmatrix}15x+30y=90\\ 15x+9y=27\end{bmatrix}`

`15x+9y=27`

`-`

`\underline{15x+30y=90}`

`-21y=-63`

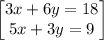
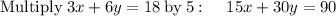
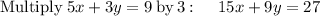
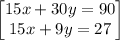
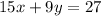
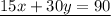
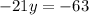
so the system of the equations becomes

`\begin{bmatrix}15x+30y=90\\ -21y=-63\end{bmatrix}`

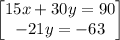
solve -21y = -63

`-21y=-63`

`\mathrm{Divide\:both\:sides\:by\:}-21`

`(-21y)/(-21)=(-63)/(-21)`

`y=3`

`\mathrm{For\:}15x+30y=90\mathrm{\:plug\:in\:}y=3`

`15x+30\cdot \:3=90`

`15x+90=90`

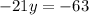
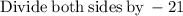
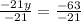
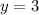
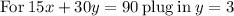
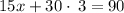
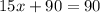
subtract 90 from both sides

`15x+90-90=90-90`

`15x=0`

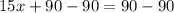
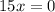
Divide both sides by 15

`(15x)/(15)=(0)/(15)`

`x = 0`

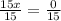
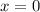
as

`x = 0`,
`y=3`

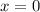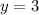
so, the system of equations contains only one solution.

Therefore, the solution of the system of equations will be:

`x=0,\:y=3`

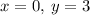
And the system of equations has ONLY ONE solution.