Answer:
When y = 0, x = -14
Thus, the x-intercept of the line is:
(x, y) = (-14, 0)
Explanation:
From the table, taking two points
(-94, 24)
(-74, 18)
Finding the slope between (-94, 24) and (-74, 18)
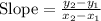
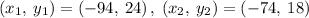
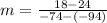
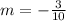
We know the slope-intercept form of line equation is
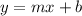
where m is the slope and b is the y-intercept
substituting m = -3/10 and the point (-94, 24) in the slope-intercept to determine the y-intercept 'b'
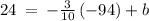
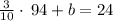
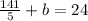
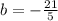
now
substituting m = -3/10 and y-intercept 'b=-21/5' in the slope-intercept of line equation
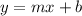
Thus, the equation of the line will be:
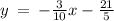
We know that the x-intercept can be determined by setting y = 0, and determining for x. so,
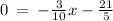
switch sides
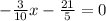
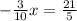
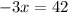
divide both sides by -3
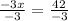
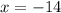
so when y = 0, x = -14
Thus, the x-intercept of the line is:
(x, y) = (-14, 0)