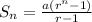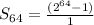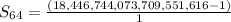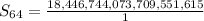Question

There are 8 rows and 8 columns, or 64 squares

on a chessboard. Suppose you place 1 penny on
Row 1 Column A, 2 pennies on Row 1 Column
B, 4 pennies on Row 1 Column C, and so on ...

Answer 1

Complete Question:

There are 8 rows and 8 columns, or 64 squares on a chessboard.

Suppose you place 1 penny on Row 1 Column A,

2 pennies on Row 1 Column B,

4 pennies on Row 1 Column C, and so on …

Determine the number of pennies in Row 1

Determine the number of pennies on the entire chessboard?

Answer:

255 in the first row

18,446,744,073,709,551,615 in the entire board

Explanation:

Given

`Rows = 8`

`Columns = 8`

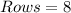
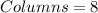
Solving (a): Number of pennies in first row

The question is an illustration of geometric sequence which follows

`1,2,4....`

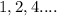
Where

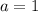`a =1` --- The first term

Calculate the common ratio, r

`r = (T_2)/(T_1) = (4)/(2) = 2`

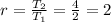
The number of pennies in the first row will be calculated using sum of n terms of a GP.

`S_n = (a(r^n - 1))/(n - 1)`

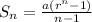
Since, the first row has 8 columns, then

`n = 8`

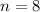
Substitute 8 for n, 2 for r and 1 for a in
`S_n = (a(r^n - 1))/(r - 1)`

`S_8 = (1 * (2^8 - 1))/(2 - 1)`

`S_8 = (1 * (256 - 1))/(1)`

`S_8 = (1 * 255)/(1)`

`S_8 = 255`

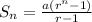
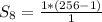
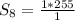
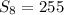
Solving (b): The entire board has 64 cells.

So:

`n = 64`

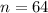
Substitute 64 for n, 2 for r and 1 for a in
`S_n = (a(r^n - 1))/(r - 1)`

`S_(64) = (1 * (2^(64) - 1))/(2 -1)`

`S_(64) = ((2^(64) - 1))/(1)`

`S_(64) = ((18,446,744,073,709,551,616 - 1))/(1)`

`S_(64) = (18,446,744,073,709,551,615)/(1)`

`S_(64) = 18,446,744,073,709,551,615`