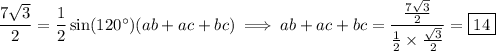Observe that
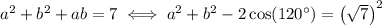
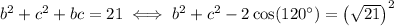
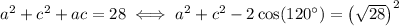
Drawing a comparison to the law of cosines, we see the first equation defines a triangle with sides
 ,
,
 , and
, and
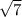 ; the second equation defines one with sides
; the second equation defines one with sides
 ,
,
 , and
, and
 ; and the third equation defines another one with sides
; and the third equation defines another one with sides
 ,
,
 , and
, and
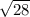 . We can then join these triangles at a point D to form a new triangle ABC with sides
. We can then join these triangles at a point D to form a new triangle ABC with sides
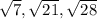 . (See attached sketch)
. (See attached sketch)
Now, the area of ABC is the sum of the areas of ABD, BCD, and ACD. The area of any of these triangles is equal to half the area of a parallelogram spanned by the sides involving the vertex D. The area of a parallelogram with adjacent sides
 and
and
 and with angle
and with angle
 between them is
between them is
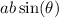 .
.
For example, triangle ABD has area

Then the total area of triangle ABC is
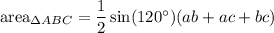
We use Heron's formula to find the area of ABC. If
 is its semiperimeter, i.e.
is its semiperimeter, i.e.

then, with a lot of algebraic simplification,
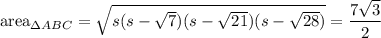
Finally, we find