Question

Each variable indicates different weights. Which weight can you find? Find it.

Record the process.
a+b+c+a+c+b+a+c=12+a+a+b+ b+c+c+c

Answer 1

We can only be certain that a weighs 12.

There are infinitely many possiblities for b and c.

Explanation:

We have the equation:

`a+b+c+a+c+b+a+c=12+a+a+b+b+c+c+c`

Each variable indicates a weight.

We would like to determine the weights of each variable (if possible).

First, we can rearrange the equation to acquire:

`(a+a+a)+(b+b)+(c+c+c)=12+(a+a)+(b+b)+(c+c+c)`

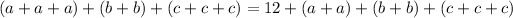
We can combine like terms:

`3a+2b+3c=12+2a+2b+3c`

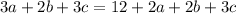
Notice that both sides have 2b and 3c. Therefore, it is possible for us to cancel them since each nullify the other side. So, we will subtract 2b and 3c from both sides. This yields:

`3a=12+2a`

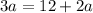
Therefore, we can solve for a. Subtract 2a from both sides:

`a=12`

Hence, the weight of a is 12.

Using the newly acquired information, we can go back to our simplified equation:

`3a+2b+3c=12+2a+2b+3c`

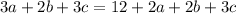
Since a is 12:

`3(12)+2b+3c=12+2(12)+2b+3c`

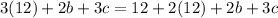
Evaluate:

`36+2b+3c=12+24+2b+3c`

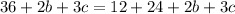
Simplify:

`36+2b+3c=36+2b+3c`

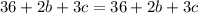
We can subtract 36 from both sides:

`2b+3c=2b+3c`

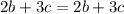
As you can see, this is a true statement.

Since this is a true statement, there are infinitely many possible values for b and c.

Therefore, the only weight we are certain of knowing is weight a weighing 12.