Answer:
The height of the pyramid is 11.8 cm to the nearest tenth of a cm
Explanation:
The formula of the volume of a pyramid is V =
× A × h, where
- A is the area of its base
∵ A right rectangular pyramid has base dimensions of 23.2 cm, 17.0 cm
∵ The area of the rectangle = Length × width
→ Assume that the length is 23.2 and the width is 17.0
∴ A = 23.2 × 17.0
∴ A = 394.4 cm²
∵ Its volume is 1552.4 cm³
∴ V = 1552.4 cm³
→ Substitute A and V in the rule above
∵ 1552.4 =
× 394.4 × h
∴ 1552.4 =
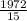h
→ Divide both sides by
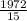
∴ 11.80831643 = h
→ Round it to the nearest tenth of a cm
∴ h = 11.8 cm
∴ The height of the pyramid is 11.8 cm to the nearest tenth of a cm