Question

An inner city revitalization zone is a rectangle that is twice as long as it is wide. The width of the region is growing at a rate of 24 m per year at a time when the region is 300 m wide. How fast is the area changing at that point in time

Answer 1

`(dA)/(dt) = 28800 \ m^2/year`

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

Geometry

• Area of a Rectangle: A = lw

Algebra I

• Exponential Property:
  `w^n \cdot w^m = w^(n + m)`

Calculus

Derivatives

Differentiating with respect to time

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Step-by-step explanation:

Step 1: Define

Area is A = lw

2w = l

w = 300 m

`(dw)/(dt) = 24 \ m/year`

Step 2: Rewrite Equation

1. Substitute in l: A = (2w)w
2. Multiply: A = 2w²

Step 3: Differentiate

Differentiate the new area formula with respect to time.

1. Differentiate [Basic Power Rule]:
   `(dA)/(dt) = 2 \cdot 2w^(2-1)(dw)/(dt)`
2. Simplify:
   `(dA)/(dt) = 4w(dw)/(dt)`

Step 4: Find Rate

Use defined variables

1. Substitute:
   `(dA)/(dt) = 4(300 \ m)(24 \ m/year)`
2. Multiply:
   `(dA)/(dt) = (1200 \ m)(24 \ m/year)`
3. Multiply:
   `(dA)/(dt) = 28800 \ m^2/year`

Answer 2

28,800 m²/yr

Explanation:

This rectangle has dimensions such that:

• width = w
• length = 2w

We are given
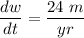`\displaystyle (dw)/(dt) = (24 \ m)/(yr)` and want to find
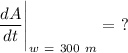`\displaystyle (dA)/(dt) \Biggr | _(w \ = \ 300 \ m) = \ ?` when w = 300 m.

The area of a rectangle is denoted by Area = length * width.

Let's multiply the width and length (with respect to w) together to have an area equation in terms of w:

• 
  `A=2w^2`

Differentiate this equation with respect to time t.

• 
  `\displaystyle (dA)/(dt) =4w \cdot (dw)/(dt)`

Let's plug known values into the equation:

• 
  `\displaystyle (dA)/(dt) =4(300) \cdot (24)`

Simplify this equation.

• 
  `\displaystyle (dA)/(dt) =1200 \cdot 24`
• 
  `\displaystyle (dA)/(dt) =28800`

The area is changing at a rate of 28,800 m²/yr at this point in time.