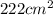Question

Find the area of following quadrilateral ​

Answer 1

A = 222 cm²

Explanation:

it is a trapezoid

so

A = ½ (a + b) h

A = ½ (16 + 21) × 12

A = ½ 37 × 12

A = ½ 444

A = 222 cm²

Answer 2

`222cm^(2)`

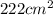
Explanation:

First we will find the length of BD.

By Pythagoras' Theorem,

`c^(2) =a^(2) +b^(2) \\BD^(2) = AD^(2) +AB^(2) \\BD^(2) =12^(2) +16^(2) \\BD^(2) = 144+256\\BD^(2) =400\\BD = √(400) \\=20cm`

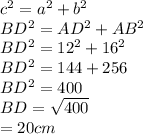
Now we will find Angle ADB.

`(AB)/(sin(Angle ADB)) =(BD)/(Sin(AngleBAD)) \\(16)/(sin(AngleADB)) =(20)/(sin(90)) \\20sin(AngleADB)=16sin(90)\\20sin(AngleADB)=16\\sin(AngleADB)=(16)/(20) \\sin(AngleADB)=0.8\\AngleADB=sin^-1(0.8)\\=53.130deg\\`

Now we will find Area of triangle BCD

`Angle BDC = 90 - Angle ADB = 90 - 53.130 = 36.87deg\\\\\\Area of Triangle BCD \\= (1)/(2) (BD)(CD)sin(AngleBDC)\\=(1)/(2) (20)(21)sin(36.87)\\= 126cm^(2)`

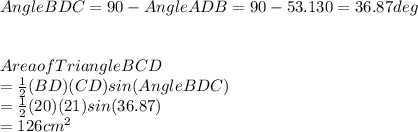
Then we will find the area of triangle BAD

`=(1)/(2) (16)(12)\\= 96cm^(2) \\`

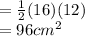
Area of quadrilateral = Area of Triangle BCD + Area of Triangle BAD

= 126+96

=
`222cm^(2)`