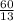Question

Whats the length in meters of CD?​

Answer 1

The length of DC in meters is
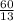`(60)/(13)` ⇒ A

Explanation:

In the circle O

∵ AB passing through O

∴ AB is a diameter

∵ D is on the circle

∴ ∠ADB is an inscribed angle subtended by arc AB

∵ Arc AB is half the circle

→ That means its measure is 180°

∴ m∠ADB =
`(1)/(2)` × 180° = 90°

In ΔADB

∵ m∠ADB = 90°

∵ AD = 5 m

∵ BD = 12 m

→ By using Pythagorase Theorem

∵ (AB)² = (AD)² + (DB)²

∴ (AB)² = (5)² + (12)²

∴ (AB)² = 25 + 144 = 169

→ Take square root for both sides

∴ AB = 13 m

∵ ∠ADB is a right angle

∵ DC ⊥ AB

∴ DC × AB = AD × DB

→ Substitute the lengths of AB, AD, and DB

∵ DC × 13 = 5 × 12

∴ 13 DC = 60

→ Divide both sides by 13

∴ DC =
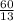`(60)/(13)` m

∴ The length of DC in meters is
`(60)/(13)`