Question

Heyy could you help me out?​

Answer 1

The mid-point M is (2, 1). M lies in quadrant I, since the x-coordinate is positive and the y-coordinate is positive

Explanation:

The coordinates of the midpoint (x, y) of the segment whose endpoints are (x1, y1) and (x2, y2) are x =
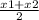`(x1+x2)/(2)` , y =
`(y1+y2)/(2)`

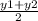
∵ M is the midpoint of DE

∵ D = (-1, 4) and E = (5, -2)

∴ x1 = -1 and x2 = 5

∴ y1 = 4 and y2 = -2

→ Use the rule above to find x, y the coordinates of M

∵ x =
`(-1+5)/(2)` =
`(4)/(2)`

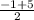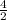
∴ x = 2

∵ y =
`(4+-2)/(2)` =
`(2)/(2)`

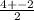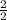
∴ y = 1

∴ The coordinates of the midpoint M are (2, 1)

∵ The x-coordinate is positive and the y-coordinate is positive

∴ M lies in the first quadrant (I)

The mid-point M is (2, 1). M lies in quadrant I, since the x-coordinate is positive and the y-coordinate is positive