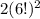Answer:
(a)12!
(b)2(6!)^2
Explanation:
(a)
well there are 12 seats so
the first seat has 12 options
the second 11
the third 10
...
the last 1
so we have
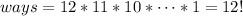
(b)
we can make two cases
case 1:
when the first one is a man
the first seat has 6 options (6 men)
the second seat has 6 options (6 women)
the third seat has 5 options (5 men)
...
the last seat has 1 option (1 woman)
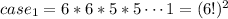
case 2
when the first one is a woman
it's the same analogy
so we have
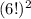
add both cases and get