Answer:
P(X = 7) = 0.11712
Explanation:
From the information given:
Average no. of claims received per week λ = 9
The required probability that exactly 7 claims will be received is determined by applying the Poisson distribution formula:
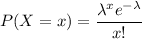
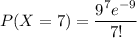
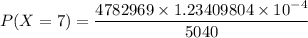
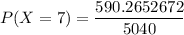
P(X = 7) = 0.11712