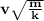Question

A block of mass m is initially moving to the right on a horizontal frictionless surface at a

speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy
of the block is equal to the potential energy of the spring, the spring is compressed a distance of:

Answer 1

Step-by-step explanation:

KE=PE

1/2mv^2=1/2kx^2

2(1/2mv^2)=2(1/2kx^2)

MV^2=kX^2

(MV^2)/k=X^2

X=√(mv^2)/k

Answer 2

The distance that the spring compresses is:

`v\sqrt{(m)/(k)}`

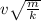
Step-by-step explanation:

Kinetic and Elastic Potential Energy

The kinetic energy of an object of mass m traveling at a speed v is:

`\displaystyle K=(1)/(2)mv^2`

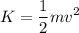
The elastic potential energy of a spring of constant k that compresses a distance x is:

`\displaystyle E=(1)/(2)kx^2`

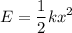
The block of mass m is moving at a speed v when compresses a spring of constant k. The kinetic energy will eventually transform into elastic energy, but before that, both energies will be equal. It happens when:

`\displaystyle (1)/(2)mv^2=(1)/(2)kx^2`

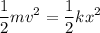
Simplifying:

`\displaystyle mv^2=kx^2`

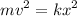
Dividing by k:

`\displaystyle x^2=(mv^2)/(k)`

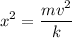
Taking square root:

`\displaystyle x=\sqrt{(mv^2)/(k)}=v\sqrt{(m)/(k)}`

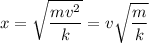
The distance that the spring compresses is
`\mathbf{v\sqrt{(m)/(k)}}`