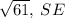Question

4. Determine the magnitude and direction of the vector v = <5, -6>.

f. 11, NE
g. 61, SE
h. 111, NE
j. V61, SE

Answer 1

The magnitude of vector is:

`\left|\begin{pmatrix}5&-6\end{pmatrix}\right|=√(61)`

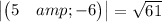
v = <5, -6> means the vector has x-coordinate x = 5 and y-coordinate y = -6, so the vector v = <5, -6> is heading towards SE.

Thus, option ( j ) is correct.

i.e.
`√(61),\:SE`

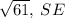
Explanation:

Given the vector

v = <5, -6>

Determining the magnitude of the vector

To find a magnitude of a vector v = (a, b) we use the formula

`||v||\:=\:√(a^2+b^2)`

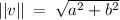
Magnitude of the vector is basically termed as the length of the vector, which is denoted by

`|\left(5,\:-6\right)|=√(\left(5\right)^2+\left(-6\right)^2)`

`=√(5^2+6^2)`

`=√(25+36)`

`=√(61)`

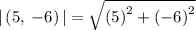
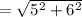
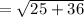
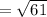
Thus, the magnitude of vector is:

`\left|\begin{pmatrix}5&-6\end{pmatrix}\right|=√(61)`

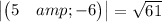
As the vector v = <5, -6> lies in 4th quadrant.

v = <5, -6> means the vector has x-coordinate x = 5 and y-coordinate y = -6, so the vector v = <5, -6> is heading towards SE.

Thus, option ( j ) is correct.

i.e.
`√(61),\:SE`