Question

Particle moves in a circle of radius 90m with a constant speed 25m/s. how many revolution does it make in 30sec​

Answer 1

n =1.33 revolutions

Step-by-step explanation:

Uniform Circular Motion

The angular speed can be calculated in two different ways:

`\displaystyle \omega=(v)/(r)`

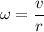
Where:

v = tangential speed

r = radius of the circle described by the rotating object

Also:

`\omega=2\pi f`

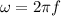
Where:

f = frequency

Solving for f:

`\displaystyle f=(\omega)/(2\pi)`

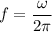
Since the frequency is calculated when the number of revolutions n and the time t are known:

`\displaystyle f=(n)/(t)`

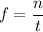
We can solve for n:

n=f.t

The particle moves in a circle of r=90 m with a speed v=25 m/s. Thus the angular speed is:

`\displaystyle \omega=(25)/(90)`

`\displaystyle \omega=0.278\ rad/s`

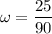
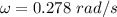
Now we calculate f:

`\displaystyle f=(0.278)/(2\pi)`

`f=0.04421\ Hz`

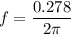
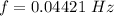
Calculating the number of revolutions:

n = 0.04421*30

n =1.33 revolutions