The order of the surd 6 √2187 after simplification is

Question

asked Oct 16, 2021 139k views

1 Answer

Chandraprakash · Answer 1 · 2021-10-20T19:55:02+0000

Answer:

n = 162

Explanation:

Given

$6\sqrt{2187$

Required

Determine the order of the surd

If a surd is represented as
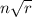$n\sqrt{r$ , then the order of the surd is

$6\sqrt{2187$

Express 2187 as
3^6 * 3

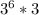
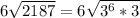
6√(2187) = 6√(3^6 * 3)

Split the surd

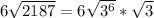
6√(2187) = 6√(3^6) * √(3)

Apply the following law of indices:

$√(a) = a^{(1)/(2)}$

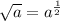
The expression becomes:

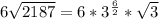
$6√(2187) = 6 * 3^{(6)/(2)} * √(3)$

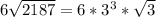
6√(2187) = 6 * 3^(3) * √(3)

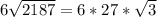
6√(2187) = 6 * 27 * √(3)

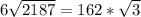
6√(2187) = 162 * √(3)

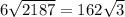
6√(2187) = 162 √(3)

By comparing
162 √(3) to
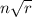$n\sqrt{r$ , we can say that:

n = 162

r = 3

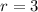
Conclusively, the order of the surd is 162