Question

Find x?
In 3x - In(x - 4) = ln(2x - 1) +ln3

Answer 1

`x = \displaystyle (5 + √(17))/(2)`.

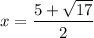Explanation:

Because
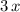`3\, x` is found in the input to a logarithm function in the original equation, it must be true that
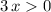`3\, x > 0`. Therefore,
`x > 0`.

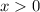Similarly, because
`(x - 4)` and
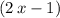`(2\, x - 1)` are two other inputs to the logarithm function in the original equation, they should also be positive. Therefore,
`x > 4`.

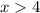Let
`a` and
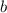`b` represent two positive numbers (that is:
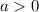`a > 0` and
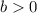`b > 0`.) The following are two properties of logarithm:

`\displaystyle \ln (a) + \ln(b) = \ln\left(a \cdot b\right)`.

`\displaystyle \ln (a) - \ln(b) = \ln\left((a)/(b)\right)`.

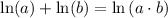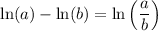Apply these two properties to rewrite the original equation.

Left-hand side of this equation:

`\begin{aligned}&\ln(3\, x) - \ln(x - 4)= \ln\left((3\, x)/(x -4)\right)\end{aligned}`

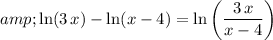
Right-hand side of this equation:

`\ln(2\, x- 1) + \ln(3) = \ln\left(3 \left(2\, x - 1\right)\right)`.

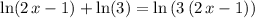Equate these two expressions:

`\begin{aligned}\ln\left((3\, x)/(x -4)\right) = \ln(3(2\, x - 1))\end{aligned}`.

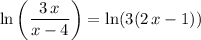The natural logarithm function
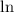`\ln` is one-to-one for all positive inputs. Therefore, for the equality
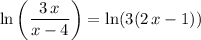`\begin{aligned}\ln\left((3\, x)/(x -4)\right) = \ln(3(2\, x - 1))\end{aligned}` to hold, the two inputs to the logarithm function have to be equal and positive. That is:

`\displaystyle (3\ x)/(x - 4) = 3\, (2\, x - 1)`.

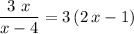Simplify and solve this equation for
`x`:

`x^2 - 5\, x + 2 = 0`.

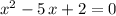There are two real (but not rational) solutions to this quadratic equation:
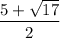`\displaystyle (5 + √(17))/(2)` and
`\displaystyle (5 - √(17))/(2)`.

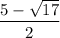However, the second solution,
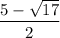`\displaystyle (5 - √(17))/(2)`, is not suitable. The reason is that if
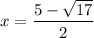`x = \displaystyle (5 - √(17))/(2)`, then
`(x - 4)`, one of the inputs to the logarithm function in the original equation, would be smaller than zero. That is not acceptable because the inputs to logarithm functions should be greater than zero.

The only solution that satisfies the requirements would be
`\displaystyle (5 + √(17))/(2)`.

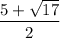Therefore,
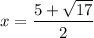`x = \displaystyle (5 + √(17))/(2)`.