Question

Help … fr …. D: D: D: D:

Answer 1

Explanation:

Let x be mixture x liters and y be mixture y liters.

We need a total of 4 liters so

`x + y = 4`

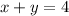
Mixture x is 20% saline solution

Mixture Y is a 10% saline solution

4 liters of a 15% saline solution is 60% saline solution.

`.20x + .10y = 0.6`

So a is the system of equations,

Using Elimination, eliminate the variable x.

`- 5(.20x + .10y) = 0.6`

`( - x - .50y) = - 3`

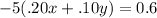
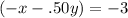
Add to the first system.

`0.50y = 1`

`y = 2`

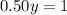
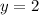
Plug this into the of system of equations, to find x

`x + 2 = 4`

`x = 2`

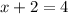
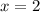
So our solution is (2,2) We would need 2 liters of Mixture X and 2 liters of Mixture Y