Answer:
Explanation:
Question (5)
Perimeter of sector APQR = AP + arc(PQR) + AR
AP = AR = 7 cm
Formula to get the length of arc(PQR) =
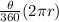
Here, r = radius of the sector
θ = Angle by the arc PQR at the center of the circle
arc(PQR) =

=
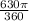
=
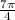
= 4.497 ≈ 4.50 cm
Perimeter of APQR = 2(7) + 4.50
= 18.50 cm
Perimeter of shaded region = BP + arc(BCD) + arc(PQR) + DR
arc(BCD) =
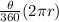
=
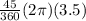
= 0.875π
≈ 2.75 cm
Perimeter of shaded region = 2(3.5) + 2.75 + 4.50
= 14.25 cm
Difference in perimeter of APQR and perimeter of shaded region = 18.50 - 14.25
= 4.25 cm
Perimeter of APQR is 4.25 cm more than the perimeter of the shaded region.
Miscellaneous question
Perimeter of remaining lamina = 2(21) + Length of arc of the remaining portion
= 42 +
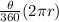
= 42 +
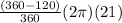
= 42 + 28π
= 42 + 87.96
= 129.96
≈ 130 cm