-------------------------------------------------------------------------------------------------------------
Answer:
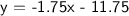
-------------------------------------------------------------------------------------------------------------
Given:
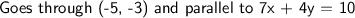
Find:
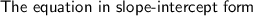
Solution: We need to first solve for y in the equation that was provided so we can determine the slope. Then we plug in the values into the point-slope form, distribute, simplify, and solve for y to get our final equation.
Subtract 7x from both sides
Divide both sides by 4
Plug in the values
Simplify and distribute
Subtract 3 from both sides
Therefore, the final equation in slope-intercept form that follows the information that was provided is y = -1.75x - 11.75