Answer:
The value of
 is approximately -1.531.
is approximately -1.531.
Explanation:
Let
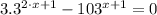 , we proceed to solve this expression by algebraic means:
, we proceed to solve this expression by algebraic means:
1)
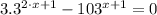 Given
Given
2)
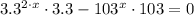
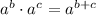
3)
![(3.3^(x))^(2)\cdot 3.3 -\left[\left( √(103) \right)^(2)\right]^(x)\cdot 103 = 0](https://img.qammunity.org/2021/formulas/mathematics/college/m6d8vt7gp68trmbkunx2lk7nmfe1bfvw53.png)
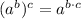
4)
![(3.3^(x))^(2)\cdot 3.3 - \left[\left(√(103)\right)^(x)\right]^(2)\cdot 103 = 0](https://img.qammunity.org/2021/formulas/mathematics/college/13d9rq4mrohpkw9sdneitutgsqe93900m3.png)
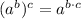 /Commutative property
/Commutative property
5)
![\left[\left((3.3)/(√(103))\right)^(x)\right] ^(2)-(103)/(3.3) = 0](https://img.qammunity.org/2021/formulas/mathematics/college/1zefdbdt2aqfr157cfovt84nxd5dc5eefd.png) Existence of multiplicative inverse/Definition of division/Modulative property/
Existence of multiplicative inverse/Definition of division/Modulative property/
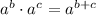
6)
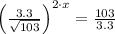 Existence of additive inverse/Modulative property/
Existence of additive inverse/Modulative property/
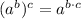
7)
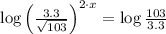 Definition of logarithm.
Definition of logarithm.
8)
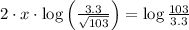
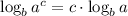
9)
![2\cdot x \cdot [\log 3.3-\log √(103)] = \log 103 - \log 3.3](https://img.qammunity.org/2021/formulas/mathematics/college/wyt3bw864ofhfdumqpbvzubk7gxsvlz8vo.png)
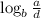
10)
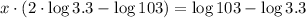
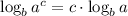 /Associative property
/Associative property
11)
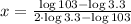 Existence of multiplicative inverse/Definition of division/Modulative property
Existence of multiplicative inverse/Definition of division/Modulative property
12)
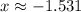 Result
Result
The value of
 is approximately -1.531.
is approximately -1.531.