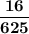Answer:
The fraction of its drop height after the fourth bounce is

Explanation:
Let's suppose the rubber ball is dropped from a height H0. Every time the ball bounces back it reaches 8/10 of the initial drop height.
The ball's height H(x) after bounce number x is:
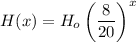
Simplifying:
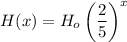
After the fourth bounce, the height is:


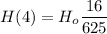
The fraction of its drop height after the fourth bounce is