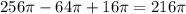Question

Help asap

short its an MCQ
If the diameter of 3 circles is in the ratio 4: 2: 1. The perimeter of the smallest circle is 8 cm. Then the area of
the shaded region is

Answer 1

216
`\pi`

Explanation:

Given the figure.

And the perimeter in the ratio 4: 2: 1.

Perimeter of smallest circle =
`8\pi`

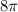
To find:

Area of shaded region.

Solution:

To find the area, we need to have radius first.

And radius can be calculated by the given perimeter.

Formula for Perimeter is given as:

Perimeter =
`2\pi r`

`8\pi = 2\pi r\\\Rightarrow r = 4\ cm`

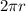
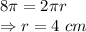
Radius of smallest circle = 4 cm

Ratio of perimeter is equal to the ratio of the radii.

Radius of 2nd smallest circle by the given ratio = 8 cm

Radius of largest circle = 16 cm

Area of a circle is given the formula:

`A = \pi r^2`

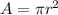
Area of the smallest circle =
`\pi 4^2 = 16\pi\ cm^2`

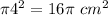
Area of the 2nd smallest circle =
`\pi 8^2 = 64\pi\ cm^2`

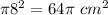
Area of the largest circle =
`\pi 16^2 = 256\pi\ cm^2`

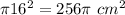
Area of the shaded region = Area of largest circle + 2
`*` Area of 2nd smallest circle + 3
`*` Area of smallest circle - 2
`*` Area of smallest circle - 3
`*` Area of 2nd smallest circle

Area of the shaded region = Area of largest circle - Area of 2nd smallest circle + Area of smallest circle =
`256\pi - 64\pi +16\pi = 216\pi`