Question

Someone, please help with this Calculus problem!!! ASAP

Answer 1

(C) 13/6

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

Point-Slope Form: y - y₁ = m(x - x₁)

• x₁ - x coordinate
• y₁ - y coordinate
• m - slope

Function Notation

Exponential Properties:
`\sqrt[n]{x} = x^(1)/(n)`

Calculus

The definition of a derivative is the slope of the tangent line.

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

f(x) = ∛x

Tangent Line Point (8, 2)

Find approximation of f(10)

Step 2: Differentiate

1. Rewrite Function:
   `f(x) = x^(1)/(3)`
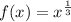
2. Differentiate [Basic Power]:
   `f'(x) = (1)/(3) x^{(1)/(3) -1}`
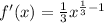
3. Simplify Derivative:
   `f'(x) = (1)/(3) x^{(-2)/(3)}`
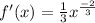
4. Rewrite Derivative:
   `f'(x) = \frac{1}{3x^{(2)/(3) }}`

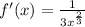
Step 3: Find Equation of Tangent Line

Tangent Point (8, 2)

Find instantaneous slope

1. Substitute in x:
   `f'(8) = \frac{1}{3(8)^{(2)/(3) }}`
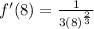
2. Exponents:
   `f'(8) = (1)/(3(4))`
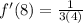
3. Multiply:
   `f'(8) = (1)/(12)`

This is our slope of the tangent line at (8, 2)

Find instantaneous equation

1. Substitute [PSF]:
   `y - 2 = (1)/(12) (x-8)`

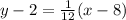
Step 4: Find Approximation

Evaluation f(10)

1. Substitute in x:
   `y - 2 = (1)/(12) (10-8)`
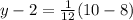
2. Subtract:
   `y - 2 = (1)/(12) (2)`
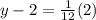
3. Multiply:
   `y - 2 = (1)/(6)`
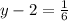
4. Isolate y:
   `y = (1)/(6) + 2`
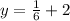
5. Add:
   `y = (13)/(6)`

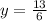
Here we see that the approximation would be 13/6 using the tangent line approximation (calculus). Therefore, C is the correct answer.