Question

The point R(-3,a,-1) is the midpoint of the line segment jointing the points P(1,2,b)

and Q(c,-7,4)
Find the values of:
a=
b=
C=

Answer 1

The values are:

• 
  `a = -5/2`

• 
  `b = -6`

• 
  `c = -7`

Explanation:

Given:

• P = (x₁, y₁, z₁) = (1, 2, b)

• Q = (x₂, y₂, z₂) = (c, -7, 4)

• m = R = (x, y, z) = (-3, a, -1)

To Determine:

a = ?

b = ?

c = ?

Determining the values of a, b, and c

Using the mid-point formula

`m\:=\:\left((x_1+x_2)/(2),\:(y_1+y_2)/(2),\:(z_1+z_2)/(2)\right)`

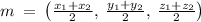
• As the point R(-3, a, -1) is the midpoint of the line segment jointing the points P(1,2,b) and Q(c,-7,4), so

• m = R = (x, y, z) = (-3, a, -1)

Using the mid-point formula

`m\:=\:\left((x_1+x_2)/(2),\:(y_1+y_2)/(2),\:(z_1+z_2)/(2)\right)`

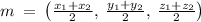
given

(x₁, y₁, z₁) = (1, 2, b) = P

(x₂, y₂, z₂) = (c, -7, 4) = Q

m = (x, y, z) = (-3, a, -1) = R

substituting the value of (x₁, y₁, z₁) = (1, 2, b) = P, (x₂, y₂, z₂) = (c, -7, 4) = Q, and m = (x, y, z) = (-3, a, -1) = R in the mid-point formula

`m\:=\:\left((x_1+x_2)/(2),\:(y_1+y_2)/(2),\:(z_1+z_2)/(2)\right)`

`\left(x,\:y,\:z\right)\:=\:\left((1+c)/(2),\:(2+\left(-7\right))/(2),\:(b+4)/(2)\right)`

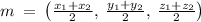
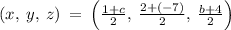
as (x, y, z) = (-3, a, -1), so

`\left(-3,\:a,\:-1\right)\:=\:\left((1+c)/(2),\:(2+\left(-7\right))/(2),\:(b+4)/(2)\right)`

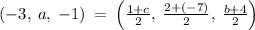
Determining 'c'

-3 = (1+c) / (2)

-3 × 2 = 1+c

`1+c = -6`

`c = -6 - 1`

`c = -7`

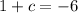
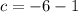
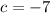
Determining 'a'

a = (2+(-7)) / 2

`2a = 2-7`

`2a = -5`

`a = -5/2`

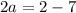
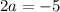
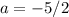
Determining 'b'

-1 = (b+4) / 2

`-2 = b+4`

`b = -2-4`

`b = -6`

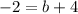
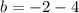
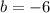
Therefore, the values are:

• 
  `a = -5/2`

• 
  `b = -6`

• 
  `c = -7`