Question

A stone is thrown vertically upwards with an initial velocity 20m/s. Find the maximum height it reaches and the time taken by it to reach the height.

(g= 10m/s)

who gives answer with explanation i will make him braillint

Answer 1

The maximum height it reaches is 20 meters

The time taken by it to reach the height is 2 seconds

Explanation:

The formula of the height of the stone is h = u t -
`(1)/(2)` g t², where

• t is the time to reach the height h

• u is the initial velocity

• g is the acceleration of gravity

∵ A stone is thrown vertically upwards with an initial velocity of 20 m/s

∴ u = 20 m/s

∵ g = 10 m/s²

→ Substitute them in the equation above

∴ h(t) = 20t -
`(1)/(2)` (10) t²

∴ h(t) = 20t - 5t²

→ Arrange the terms of the right side according to the greatest power of t

∴ h(t) = -5t² + 20t

To find the maximum height and the time of it find the vertex of the quadratic function (m, k), where m =
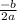`(-b)/(2a)` and k is the value of h at t = m, a is the coefficient of t² and b is the coefficient of t

∵ The coefficient of t² is -5

∴ a = -5

∵ The coefficient of t is 20

∴ b = 20

→ Use them to find h

∵ m =
`(-20)/(2(-5))` =
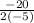`(-20)/(-10)` = h

∴ m = 2

→ Substitute it in the equation above to find k

∵ h(m) = k

∵ k = -5(2)² + 20(2)

∴ k = -5(4) + 40

∴ k = -20 + 40

∴ k = 20

∴ The coordinate of the vertex of the function are (2, 20)

→ m represents the time of the maximum height and k represents

the maximum height

∴ The maximum height it reaches is 20 meters

∴ The time taken by it to reach the height is 2 seconds