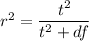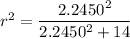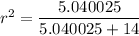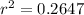Answer:
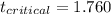
t = 2.2450
d. 0.264
Explanation:
The null hypothesis is:
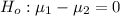
Alternative hypothesis;
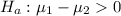
The pooled variance t-Test would have been determined if the population variance are the same.
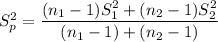
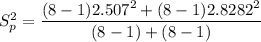
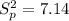
The t-test statistics can be computed as:
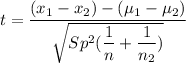
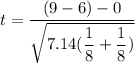
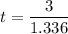
t = 2.2450
Degree of freedom
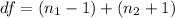
df = (8-1)+(8-1)
df = 7 + 7
df = 14
At df = 14 and ∝ = 0.05;
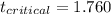
Decision Rule: To reject the null hypothesis if the t-test is greater than the critical value.
Conclusion: We reject
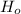 and there is sufficient evidence to conclude that the test scores for contact address s less than Noncontact athletes.
and there is sufficient evidence to conclude that the test scores for contact address s less than Noncontact athletes.
To calculate r²
The percentage of the variance is;