Question

3. Nick lifts 2 buckets of water up to the roof of his school. He plans to drop the water on his physics teacher. The 2 buckets are hung one above the other and pulled up the roof by a rope. The mass of the top bucket and its water is 9.00 kg, and the bottom bucket and its water has a mass of 6.00 kg. If the action reaction force between the buckets (the tension in the rope between the buckets) is 70.0 N, calculate:

a) the acceleration [3]
b) the force applied by Jack to lift the 2 buckets up. [2]

Answer 1

a. The acceleration of the buckets is 1.8
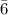`\bar 6` m/s²

b) The force applied by Jack is 175 N

Step-by-step explanation:

a. The given parameters are;

The mass of the top bucket and the water it contains, m₁ = 9.00 kg

The mass of the top bucket and the water it contains, m₂ = 6.00 kg

The tension in the rope between the buckets = 70.0 N

The tension in the rope between the buckets = The upward pulling force applied by Jack + The downward acting weight of the lower bucket

The upward pulling force applied by Nick on the lower bucket = F = m₂ × a

Where;

a = The acceleration given to the two buckets

∴ F = 6.00 kg × a

The downward acting weight of the lower bucket = m₂ × The acceleration due to gravity, g

∴ The downward acting weight of the lower bucket = 6.00 kg × 9.8 m/s² = 58.8 N

Which gives;

The tension in the rope between the buckets = 70.0 N = 6.00 kg. × a + 58.8 N

From which we have;

70.0 N = 6.00 kg. × a + 58.8 N

6.00 kg. × a = 70.0N - 58.8 N = 11.2 N

a = 11.2 N/(6.00 kg) = 1.8
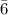`\bar 6` m/s²

The acceleration, a = 1.8
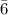`\bar 6` m/s²

b) The force applied by Jack, F = The force moving the buckets up + The weights of the buck

∴ The force applied by Jack, F = Total mass × Acceleration + Weight of the two buckets

The force applied by Jack, F = (9.00 kg + 6.00 kg) × 1.8
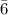`\bar 6` m/s² + (9.00 kg + 6.00 kg) × 9.8 m/s². = 28 N + 147 N = 175 N.