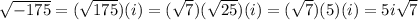Question

4. When simplified, what is the value of 175, if i2 = – 1.

Answer 1

`5i√(7)`

Explanation:

In order to solve this question we need to know how to multiply roots. You will need to understand that when we multiply
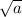`√(a)` by
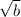`√(b)`, the following is true.

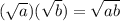`(√(a))(√(b)) = √(ab)` (1)

From the question it self we know that
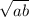`√(ab)` is equal to
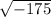`√(-175)`. We also know that
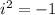`i^(2) = -1` or in other words
`i = √(-1)`.

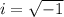Now we will need to factors
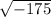`√(-175)` so that at the end we will end up representing
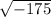`√(-175)` as a product of
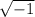`√(-1)` and some other number. In order to determine the unknown number we will just have to divide
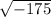`√(-175)` by
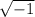`√(-1)`. From the equation (1) that I mention at the start we can figure out that......

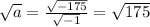`√(a) = (√(-175) )/(√(-1) ) = √(175)` (in our case
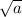`√(a)` is the unknown number we are trying to find)

Now we can rewrite
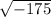`√(-175)` as the following.....

`√(-175) = (√(175))(√(-1))`

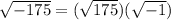
From here we substitute
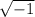`√(-1)` with
`i` and simplify
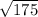`√(175)`. In order to simplify
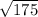`√(175)` we will have to factor
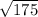`√(175)` in a way that we will see
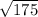`√(175)` as a multiple of a perfect square root. An so we get the following

`√(-175) = (√(175))(i) = (√(7))(√(25) )(i) = (√(7))(5)(i) = 5i√(7)`

Answer 2

5i
`√(7)`

Explanation:

Using the rule of radicals

`√(a)` ×
`√(b)` ⇔
`√(ab)`

i² = - 1 ⇒ i =
`√(-1)`

Given

`√(-175)`

=
`√(25(7)(-1))`

=
`√(25)` ×
`√(7)` ×
`√(-1)`

= 5i
`√(7)`